Métriques des LLM : mesurer leurs performances

Une des difficultés lors de la création des LLM est de pouvoir mesurer efficacement leurs performances. En effet, contrairement à la plupart des algorithmes de Machine Learning classiques qui cherchent à prédire des quantités ou des modalités/classes, un LLM va quant à lui proposer du texte en réponse, dont le nombre de mots n'est pas connu à l'avance. Il peut donc être difficile de déterminer une métrique

En règle générale, il existe des métriques pour mesurer la qualité d'un LLM sur des tâches précises : pour la prédiction du mot suivant à partir des précédents, pour la qualité de la traduction, ou encore pour le résumé de texte. Il est donc souvent d'usage de ne pas calculer une seule métrique, mais d'en calculer plusieurs et d'effectuer des agrégations pour déterminer le meilleur LLM si l'on souhaite obtenir un modèle plutôt général.

Dans cet article, nous allons faire un tour d'horizon des principales métriques que l'on peut être amené à utiliser avec les LLM, ainsi que les jeux de données régulièrement présents dans les benchmarks.

Métriques d'évaluation de LLM

L'évaluation des LLM est une étape critique avant de pouvoir le mettre à disposition d'utilisateurs ou de collaborateurs. En effet, elles vont non seulement permettre de comparer les différents modèles sur la base de critères établis, mais aussi de mesurer les progrès et les évolutions à travers le temps.

On peut distinguer deux critères différents pour mesurer les performances.

Des critères qualitatifs, où l'on utilise des exemples bien connus pour mesurer qualitativement la réponse d'un LLM. Le plus souvent, ce critère se base sur des décisions humaines, où l'on sera capable d'indiquer si la réponse obtenue est correcte ou non. Ces critères sont bien entendu sujets à des biais, puisque la décision peut dans certains cas dépendre de l'interprétation de la réponse. On retrouve ainsi plutôt ses critères dans les tests de sécurité ou pour le renforcement post-entraînement.
Des critères quantitatifs, où l'on utilise des calculs statistiques pour obtenir un ou plusieurs scores. Ces scores, souvent compris entre 0 et 1, permettent alors de comparer facilement les modèles entre-eux, mais il convient de fixer une métrique adaptée à chaque problématique pour calculer des scores qui ont du sens.

Même si certaines métriques comme le $F1$-score peuvent être utilisées dans des situations simples comme de la question-réponse, d'autres sont particulièrement adaptées pour la génération de réponses en langage naturel. C'est le cas des métriques de perplexité, ROUGE ou encore BLEU que nous allons détailler.

Perplexité

La perplexité fait partie des métriques les plus utilisées pour évaluer les performances des LLM. En effet, elle pourrait être celle qui se rapproche le plus d'une évaluation naturelle, car elle permet de quantifier la capacité d'un LLM à prédire un échantillon de texte.

De manière informelle, la perplexité mesure à quel point le modèle « est surprisr » lorsqu'il découvre un nouveau texte. Lorsque la perplexité est basse, cela indique que le modèle n'a aucune difficulté à prédire correctement le texte attendu, même pour un texte qu'il n'a jamais vu auparavant.

Le calcul de la perplexité se base sur l'entropie croisée (cross entropy) entre la distribution actuelle (le texte attendu) et la distribution prédite (la réponse du LLM).

Concrètement, pour une séquence $X=(x_1, \dots, x_2)$ de $t$mots à prédire, on détermine la probabilité que le $i$-ème mot soit $x_i$, à partir de la séquence connue $x_{<i}=(x_1, \dots)$ jusqu'ici.

$$\text{PPL}(X)=\exp \large\left\{ -\frac{1}{t} \sum_{i=1}^t \log p_{\theta} (x_i | x_{<i}) \large \right\}$$

Ici, $\log p_{\theta} (\dots)$ est la log-vraisemblance du $i$-ème mot à partir des mots précédents. Un modèle avec une faible perplexité sera donc capable de correctement prédire$x_i$sachant $x_{i-1}$, et donc la log-vraisemblance sera d'autant plus faible.

En général, la perplexité est une métrique plutôt utiliser pour déterminer à quel point un LLM a bien été entraîné sur un corpus. Dans l'image ci-dessous, nous voyons que la distribution agit comme une fenêtre glissante tout au long de la réponse du modèle.

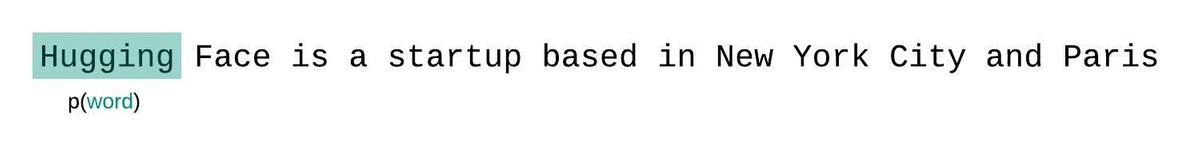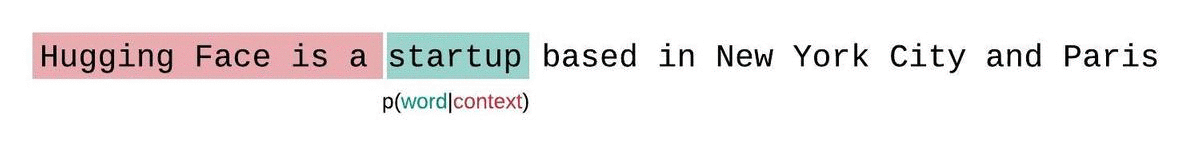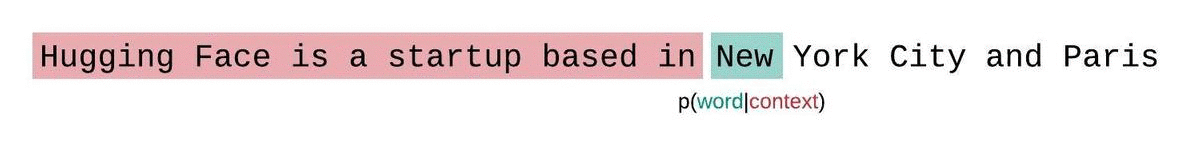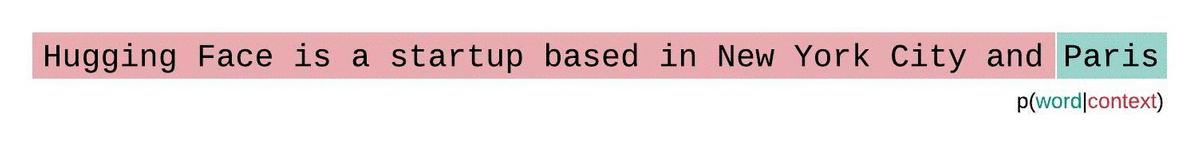
Dans les faits, la perplexité est relativement simple à calculer, car il suffit de vérifier que le prochains mots prédits à partir du contexte est le bon. En revanche, cette méthode va être sensible aux informations qui ne sont pas disposées dans le même ordre

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

ROUGE est une autre métrique principalement utilisée pour évaluer la qualité des résumés de texte. En effet, ROUGE utilise la notion de n-grammes, les mots en séquences ainsi que les sous-séquences qui apparaissent dans le texte résumé.

Pour chaque texte à résumer, on dispose de références, qui peuvent être un ou plusieurs textes résumés du texte initial. Le candidat est alors la proposition de résumé faite par le LLM.

$$ \text{Recall}=\frac{\text{Overlapping n-grams}}{\text{Number of n-grams in reference}} \qquad \text{Precision}=\frac{\text{Overlapping n-grams}}{\text{Number of n-grams in candidate}} $$

À partir de là, le calcul est ensuite un simple $F1$-score.

$$ F1=2 \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$

Il existe plusieurs variantes de ROUGE en fonction de la valeur de$n$pour déterminer les n-grammes à utiliser. Prenons quelques exemples de variantes de ROUGE.

ROUGE-1

La métrique ROUGE-1 utilise uniquement des uni-grammes, c'est-à-dire n'utilise que la présence ou non de chaque mot obtenu dans la références. Supposons que nous disposons d'un texte à deux références, le candidat étant la proposition faite par le LLM.

Reference 1 : Hello world on this website
Reference 2 : Hello everyone on Blent
Candidate : Welcome everyone on Blent website

Afin de comparer efficacement les résumés, on utilise en général la référence avec le plus de chevauchement d'uni-grammes du candidat, qui est ici la deuxième référence.

Reference 1 : (Hello), (world), (on), (this), (website)
Reference 2 : (Hello), (everyone), (on), (Blent)
Candidate : (Welcome), (everyone), (on), (Blent), (website)

En comparant la référence 2 avec le candidat, il y a 3 mots sur 4 du candidat présents dans la référence : le rappel est de $0.75$. En revanche, seuls 3 mots de la référence sont présents parmi les 5 du candidats, donc la précision est de $0.6$. Ainsi, le $F1$-score pour ce texte est d'environ $0.67$.

En effectuant la moyenne de tous les $F1$-score pour tous les candidats présents dans le jeu de données, nous obtenons la valeur de la métrique ROUGE-1.

ROUGE-2

Dans le cas de la métrique ROUGE-2, on n'utilise plus cette fois-ci les uni-grammes mais les bi-grammes : ce sont dorénavant des séquences de couples de mots qui sont utilisés. Ainsi, le calcul doit être fait sur l'intégralité des séquences, c'est-à-dire que la séquence d'une référence doit être identique à celle que l'on peut trouver dans le candidat pour être considéré comme un chevauchement.

Reference 1 : (Hello, world), (world, on), (on, this), (this, website)
Reference 2 : (Hello, everyone), (everyone, on), (on, Blent)
Candidate : (Welcome, everyone), (everyone, on), (on, Blent), (Blent, website)

Ici, nous voyons que 2 séquences du candidats sont présents parmi les 3 séquences de la référence, ce qui donne un rappel (arrondi supérieur) de $0.67$. À l'inverse, il y a aussi 2 séquences de la référence dans les 5 séquences du candidat, soit une précision de $0.4$. Le $F1$-score est donc de $0.5$.

Également ici, la moyenne de tous les $F1$-score permet d'obtenir la valeur de la métrique ROUGE-2.

ROUGE-n

Par extension, la métrique ROUGE-n permet d'effectuer les mêmes opérations mais en considérant des séquences de n-grammes. Évidemment, plus la valeur de $n$est élevée, plus les séquences qui doivent être exactement retrouvées entre la référence et le candidat sont grandes.

À noter qu'il existe d'autres variantes de la métrique ROUGE, comme ROUGE-L qui se base sur la sous-séquence commune la plus longue, ou encore ROUGE-S qui utilise les skip-grams plutôt que des n-grammes.

BLEU (Bilingual Evaluation Understudy)

BLEU est une métrique principalement utilisée pour évaluer la qualité de la traduction entre deux langues. Tout comme ROUGE, cette métrique utilise également le concept de n-grammes ainsi que le calcul de la précision, mais apporte une modification sur cette dernière pour éviter le problème suivant.

Reference : (Hello), (world), (on), (this), (website)
Candidate : (Hello), (Hello), (Hello), (Hello), (Hello)

Ici, nous avons 5 fois le même mot qui apparaît dans le candidat (réponse du LLM). Puisque les 5 mots (identiques) apparaissent parmi les 5 mots de la référence, la précision est de 1... ce qui n'est pas vraiment réaliste ici puisque le LLM ne fait que répéter le même mot à chaque fois !

Pour pallier à ce problème, BLEU calcule la notion de Modified Precision$p_n$. La solution pour contourner ce problème, c'est de tronquer le nombre d'occurrences d'un mot dans le candidat par rapport à la référence, noté ici $\text{MaxRefCount}$.

$$ \text{Count}_{\text{Clip}}=\min(\text{Count}, \text{MaxRefCount}) $$

Dans notre exemple, le mot Hello n'apparaît qu'une seule fois dans la référence, ce qui donne $\text{Count}_{\text{Clip}}=\min(5,1)=1$. Ainsi, la valeur de $p_n$ici est égale à $\frac{1}{5}=0.2$.

Un autre problème qui peut survenir est lorsque les phrases du candidat sont plus petites que celles de la référence. Dans cette situation, BLEU calcule également le Brevity Penalty pour pénaliser les prédictions trop courts par rapport aux références. Il s'agit simplement d'un calcul qui compare la longueur (nombre de mots) de ma référence $r$avec celle du candidat $c$.

$$\text{BP}=\left\{\begin{matrix} 1 & \text{si } c > r \\ \exp(1-\frac{r}{c}) & \text{si } c \leq r \\ \end{matrix}\right.$$

À partir d'ici, la métrique BLEU se calcule comme une moyenne géométrique, en calculant la Modified Precision $p_n$pour tous les n-grammes de 1 à $N$(étant ici le $n$maximum de n-grammes que l'on peut former) et $w_1, \dots, w_N$des pondérations dont la somme vaut 1.

$$ \text{BLEU}=\text{BP} \exp \large \left( \sum_{i=1}^N w_n \log p_n \large \right) $$

L'intérêt des pondérations est de ne pas considérer certains n-grammes qui seraient trop grands ou trop petits par exemple. Ainsi, on pourrait privilégier les bi-grammes ou tri-gramme au détriment des n-grammes d'ordres supérieurs. Dans la pratique, le calcul de la métrique BLEU se limite souvent jusqu'aux tétragrammes (4 mots).

Jeux de données d'évaluation

La qualité d'une évaluation d'un LLM dépend également du jeu de données utilisé pour le tester. En effet, celui-ci doit être varié, suffisamment représentatifs pour la problématique que l'on souhaite résoudre, et surtout de grande qualité pour garantir une évaluation fiable.

À découvrir : notre formation LLM Engineering

Il peut donc y avoir un travail important de retraitement de données et d'adaptation à un contexte particulier qu'il faut prendre en compte pour évaluer un LLM. Afin de faciliter les comparaisons entre les LLM via des benchmarks, il existe plusieurs jeux de données publics.

GLUE (General Language Understanding Evaluation) et SuperGLUE : ces jeux de données génériques sont conçus pour mesurer la capacité d'un modèle à comprendre le texte. Ils comprennent notamment des tests couvrant des aspects comme la compréhension de la lecture, l'inférence de sens, et la reconnaissance des entités nommées (NER).
SQuAD (Stanford Question Answering Dataset) : ce jeu de données est populaire pour évaluer la compréhension de la lecture où un modèle doit répondre aux questions en se basant sur des paragraphes donnés.
Common Crawl : un corpus très grand de données collectées sur le Web, et utilisé pour l'entraînement de LLM. Il offre une diversité linguistique et thématique qui est essentielle pour la généralisation des modèles.
MultiNLI (Multi-Genre Natural Language Inference) : un autre corpus qui favorise cette fois-ci l'évaluation de la capacité d'un modèle à faire des inférences sur des paires de phrases afin d'établir s'il y a contradiction, neutralité, ou affirmation.
WMT (Workshop on Statistical Machine Translation) : utilisé principalement pour évaluer les tâches de traduction automatique, il comprend un ensemble de paires de phrases dans plusieurs langues avec leurs traductions de référence.

Conclusion

Comme nous venons le voir, il n'existe pas une métrique universelle qui permet de mesurer tous les LLM : il faudra toujours utiliser une métrique spécifique qui répond à un besoin précis, comme la traduction ou le résumé de textes. Si l'on souhaite néanmoins proposer un modèle qui puisse généraliser à un ensemble de tâches assez important, l'usage est donc de calculer plusieurs métriques et d'effectuer une moyenne finale pour toujours comparer les différentes versions entre-elles.