
Par Équipe Blent
Data Scientist
Publié le 21 févr. 2022
Catégorie Machine Learning
L’ACP : tout savoir sur l’Analyse en Composantes Principales
Si vous avez déjà travaillé avec des jeux de données contenant beaucoup de variables, vous savez que cela peut présenter des problèmes. Comprenez-vous toutes vos variables et les relations entre-elles ? Avez-vous tellement de variables que vous risquez de surcharger ou sur-apprendre votre modèle ?
Pour éviter tout cela, les Data Scientists ont recours généralement à l'ACP ou l’Analyse en Composantes Principales. C’est une méthode de réduction de la dimensionnalité qui améliore la performance des algorithmes de Machine Learning car elle élimine les variables corrélées qui ne contribuent à aucune prise de décision.
Dans cet article, nous allons détailler la notion de réduction des dimensions, le fonctionnement de l’ACP, comment et quand faut-il l’utiliser.
Notion de la réduction des dimensions en Machine Learning
La réduction de dimension est un processus étudié en mathématiques et en informatique. Il consiste à prendre des données dans un espace de grande dimension, et à les remplacer par d'autres dans un espace de dimension inférieure, mais qui contiennent encore la plupart des renseignements contenues dans le grand ensemble.
Autrement dit, on cherche à construire moins de variables tout en conservant le maximum d'informations possible.
En Machine Learning, ce processus de traitement de données est crucial dans certains cas, parce que les jeux de données plus petits sont plus faciles à explorer, exploiter et à visualiser, et rendent l’analyse des données beaucoup plus facile et plus rapide.
À lire aussi : découvrez notre formation MLOps
Cette étape est importante aussi dans les cas du sur-apprentissage et des données très éparses (fléau de la dimensionnalité), qui nécessitent beaucoup de temps et de puissance de calcul pour les étudier.
En utilisant un espace de plus petite dimension, on obtient des algorithmes plus efficaces, ainsi qu'un panel de solutions plus réduit.
En Data Science, il existe aujourd'hui plusieurs méthodes et techniques pour réduire la dimension d'un ensemble de données. Chaque méthode est utilisée dans des cas spécifiques et avec des types de données précis. Parmi ces méthodes on peut citer:
SVD (Singular Value Decomposition)
En Machine Learning, l'un des concepts les plus importants d’algèbre linéaire est la décomposition de valeur singulière (SVD). L’idée est de décomposer une matrice dans le produit unique de 3 autres matrices.
SVD est similaire à L'ACP, mais plus générale. L'ACP suppose que la matrice d'entrée est carré, alors que SVD n’a pas cette hypothèse. La formule générale de SVD est
$$M=U\Sigma V^{\top}$$- \(M\) est la matrice originale que nous voulons décomposer.
- \(U\) est une matrice singulière gauche (les colonnes sont des vecteurs singuliers gauches).
- \(\Sigma\) est une matrice diagonale contenant des valeurs singulières.
- \(V\) est une matrice singulière droite (les colonnes sont des vecteurs singuliers droits).
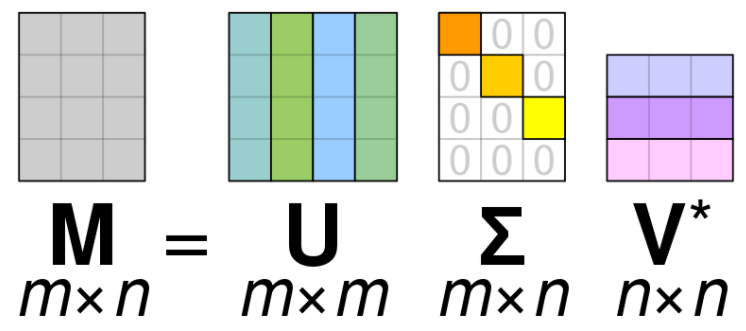
On peut dire maintenant dire que \(\Sigma\) est une compression de \(M\), cette méthode est utilisée généralement pour compression d’image et débruitage des données.
Les auto-encodeurs
Ce sont des réseaux de neurones qui visent à copier leurs sorties sur leurs entrées. Ils fonctionnent en comprimant l’entrée dans une représentation d’espace latent, puis en reconstruisant la sortie à partir de cette représentation. Ce type de réseau est composé de trois parties :
- Encodeur : C’est la partie du réseau qui compresse l’entrée en une représentation d’espace latent. Il peut être représenté par une fonction d’encodage \(h=f(x)\).
- Décodeur : Cette partie vise à reconstruire l’entrée à partir de la représentation d’espace latent. Elle peut être représentée par une fonction de décodage \(r=g(h)\).
- Une couche dense au milieu ou un espace latent (de taille bien inférieure à la couche d'entrée ou la couche de sortie) : c'est cette couche qui nous permet de faire la compression, cette couche contient les mêmes données de la couche encodeur mais en dimension plus petite.

Cette méthode est généralement utilisée avec dans la Computer Vision pour la génération d'images.
La sélection des variables
La sélection des variables (ou Feature Selection en englais), est le processus de sélection des variables les plus importantes à utiliser dans les algorithmes Machine Learning.
Des techniques de sélection des variables sont utilisées pour réduire le nombre de variables d’entrée en éliminant les fonctionnalités redondantes ou non pertinentes pour le modèle. Parmi ces techniques on peut citer:
- Les méthodes d’encapsulation calculent les modèles avec un certain sous-ensemble de caractéristiques et évaluent l’importance de chaque caractéristique. Puis ils itèrent et essaient un sous-ensemble différent de fonctionnalités jusqu’à ce que le sous-ensemble optimal soit atteint.
- La méthode de coefficient de corrélation consiste à calculer toutes les corrélations et choisir les caractéristiques qui ont la corrélation la plus élevée avec la variable qui sera prédite.
La Feature Selection est l’approche la plus connue parmi celles de réduction de dimensionnalité. Plusieurs autres peuvent être citées en guise d'exemple comme la réduction avec la cartographie isométrique, la LDA (Linear Discriminant Analysis), l'algorithme t-SNE (t-distributed Stochastic Neighbor Embedding), et bien évidemment l'ACP.
Fonctionnement de l'ACP
L’analyse des composantes principales, ou ACP, est une méthode de réduction de la dimensionnalité qui est souvent utilisée pour transformer un grand ensemble de variables en un ensemble plus petit qui contient encore la plupart des renseignements dans le grand ensemble. On parle aussi souvent de PCA, de son nom anglais Principal Components Analysis.
L'idée est de transformer des variables corrélées en nouvelles variables décorrélées en projetant les données dans le sens de la variance croissante. Les variables avec la variance maximale seront choisies comme les composants principaux.
À lire aussi : découvrez notre formation MLOps
Pour faire cela, on doit tout d'abord trouver une nouvelle base orthonormée dans laquelle on va représenter nos données, telle que la variance de ces données selon ces nouveaux axes est maximisée.
Prenons l'exemple suivant.

On remarque ici, dans le premier repère, que la variance des données selon l'axe rouge est grande. Si on projette les points sur cet axe, ils auront tous des coordonnées différentes mais on continue à pouvoir distinguer les points les uns des autres, en utilisant cet axe comme unique dimension, on réduit la dimension de nos données (de 2 à 1).
Prenons un autre exemple plus détaillée pour expliquer l'ACP étape par étape.
- Supposons qu'on dispose du jeu de données à 4 variables et 5 observations d'entrainement ci-dessous.

La première étape consiste à normaliser son ensemble de données en utilisant la formule suivante: latex
X'=\frac{X-\mu}{\sigma}
On va commencer par calculer la moyenne et l'écart-type de chaque variable.

On obtient les données suivantes après avoir appliquer la formule précédente sur tous les observations.

L'étape suivante consiste à calculer la matrice de covariance comme suit.

Puisqu'on a normalisé l'ensemble de données, ce dernier est maintenant centré, c'est-à-dire que la moyenne de ses colonnes est 0 et l'écart-type est égale à 1.
Dans la suite, on va calculer les valeurs propres et les vecteurs propres. Soit \(A\) une matrice carrée (dans notre cas c'est la matrice de covariance), \(v\) un vecteur et \(\lambda\) un scalaire qui satisfait \(Av=\lambda v\), alors \(\lambda\) est appelée valeur propre associée au vecteur propre\(v\) de \(A\).
$$(A-\lambda) ν = 0$$Puisque nous savons déjà que \(v\) est un vecteur non nul, seule cette équation peut être égale à zéro, si
$$\det (A-\lambda) = 0$$Après avoir calculer toutes les valeurs propres de notre matrice, pour chaque valeur on va retrouver les vecteurs propres associées en résolvant de l'équation \((A-\lambda I_d)v=0\) pour le vecteur \(v\) avec différentes valeurs \(\lambda\).
Ensuite, on trie les valeurs propres et leurs vecteurs propres correspondants et on choisit \(k\) valeurs propres pour former une matrice de vecteurs propres. Dans notre cas on va choisir deux vecteurs propres. On les utilisera pour transformer la matrice de covariance d'origine avec la formule suivante:
`Matrice de caractéristiques k vecteurs propres = données transformées`*
Les données obtenues ne forment plus une matrice carrée mais plutôt une matrice de taille \(m \times k\), \(k\) étant le nombre de vecteurs propres choisis (\(k=2\) dans notre cas) , et m la taille d'origine de la matrice. On a donc réussi à convertir nos données de 4 dimensions en 2 dimensions.
Nous avons pu utiliser comme nouvelles dimensions la base formée par les vecteurs propres de la matrice de covariance des données.
Comment choisir le nombre de composantes principales ?
Une partie essentielle de l’utilisation de l’ACP en pratique est la capacité d’estimer le nombre de composantes nécessaires pour décrire les données. La méthode qu'on vient d'expliquer permet de construire autant de composantes principales ou de vecteurs propres que le nombre de variables de son jeu données.
Mais le choix du nombre de composantes à utiliser était fait intuitivement. Comment faire pour trouver le \(k\) optimal pour ses données ? \(k\) peut être estimé en examinant le ratio de variance expliquée cumulatif en fonction du nombre de composantes.
Le ratio de la variance expliquée est le pourcentage de la variance attribuée à chacune des composantes sélectionnées.
À lire aussi : découvrez notre formation MLOps
Cette visualisation est obtenue directement à l'aide de la libraire matplotlib et scikit-learn avec la méthode explained_variance_ratio.

L’emplacement d’une inflexion dans le graphique est généralement considéré comme un indicateur du nombre approprié de composantes. Dans la courbe ci-dessus, le nombre de composantes adéquat est 10.
Applications de l'ACP
L'ACP est une technique de Machine Learning très utilisée par les Data Scientists. Elle intervient dans de nombreuses situations ou le jeu de données en question est compliqué et difficile à décortiquer.
- L'étude des corrélations entre les variables, afin d'éventuellement réduire le nombre de variables à utiliser avec le modèle par la suite.
- L'obtention de facteurs non corrélés qui sont des combinaisons linéaires des variables de départ, afin d'utiliser ces facteurs dans des méthodes de modélisation telles que la régression linéaire, la régression logistique ou l'analyse discriminante .
- La visualisation des observations dans un espace ou une base à deux ou trois dimensions, pour identifier des groupes d'observations homogènes, ou au contraire des observations atypiques.
L'ACP est donc une méthode de réduction de la dimensionnalité qui permet non seulement d'éviter le sur-apprentissage, mais aussi de simplifier les données et de gagner en matière de temps et de puissance de calcul.
Articles similaires

20 sept. 2022
Hugging Face est une startup française qui s'est fait connaître grâce à l'infrastructure NLP qu'ils ont développée. Aujourd'hui, elle est sur le point de révolutionner le domaine du Machine Learning et traitement automatique du langage naturel. Dans cet article, nous allons présenter Hugging Face et détailler les taches de base que cette librairie permet de réaliser. Nous allons également énumérer ses avantages et ses alternatifs.
Équipe Blent
Data Scientist
Lire l'article

12 juil. 2022
spaCy est une bibliothèque open-source pour le traitement avancé du langage naturel. Elle est conçue spécifiquement pour une utilisation en production et permet de construire des applications qui traitent et comprennent de grands volumes de texte.
Équipe Blent
Data Scientist
Lire l'article

4 juil. 2022
Un auto-encodeur est une structure de réseaux neuronaux profonds qui s'entraîne pour réduire la quantité de données nécessaires pour représenter une donnée d'entrée. Ils sont couramment utilisés en apprentissage automatique pour effectuer des tâches de compression de données, d'apprentissage de représentations et de détection de motifs.
Équipe Blent
Data Scientist
Lire l'article

60 rue François 1er
75008 Paris
Blent est une plateforme 100% en ligne pour se former aux métiers Tech & Data.
Organisme de formation n°11755985075.

Data Engineering
IA Générative
MLOps
Cloud & DevOps
À propos
Gestion des cookies
© 2025 Blent.ai | Tous droits réservés
