Interprétabilité et Machine Learning

Ce sont des mots que l'on entend de plus en plus : transparence et audit des algorithmes, modèles boîtes noires ou encore interprétabilité. Ce vocabulaire n'est pas tout récent, car déjà au tout début des années 2000, des chercheurs avaient proposé des méthodes permettant d'expliquer le comportement de certains algorithmes dont le fonctionnement était opaque, difficile à traduire en terme de décisions. Par ailleurs, plusieurs secteurs d'activité comme le secteur bancaire, de l'assurance ou de la santé n'ont pas attendu pour intégrer dès le début des méthodes de transparence.

Mais alors, pourquoi l'interprétabilité est un enjeu aussi crucial ? Avant de rentrer dans les détails, prenons un exemple pour bien comprendre les aboutissants de l'interprétabilité.

Supposons qu'une personne de 38 ans, mariée et avec 2 enfants, souhaite souscrire à un prêt immobilier. Plutôt que d'évaluer sa solvabilité manuellement, on laisse un algorithme le faire à notre place. Cet algorithme doit fournir une réponse adaptée, c'est-à-dire une réponse positive si la personne est solvable, ou une réponse négative dans le cas contraire. En pratique, l'algorithme produira une probabilité qui indique à quel point il est probable que la personne soit solvable.

À lire aussi : découvrez notre formation MLOps

Nous avons construit le modèle à partir de données sur un historique de 10 ans (avec à la fois des dossiers solvables et non solvables), et le modèle fournit la probabilité de 80%. Plusieurs interrogations surviennent :

• À quel point a-t-on confiance dans le 80% ? Et si le modèle avait autant de « chances » de produire 50% que 80%, quelle confiance pourrions-nous accorder à cette réponse ?
• Qu'est-ce qui justifie 80% ? Est-ce que c'est parce qu'il est marié, ou qu'il a 38 ans ? Voir les deux ?
• Est-ce que ce profil n'est pas valorisé par rapport à mon historique ? S'il y a un sur-représentation de dossiers solvables avec les mêmes caractéristiques, est-ce que l'on ne priorise pas ce genre de profils par rapport à d'autres qui auraient les même garanties mais seraient plus « atypiques » ?

Et c'est bien là tout le problème : en théorie, rien ne nous permet de répondre à ces questions. Il faut visualiser le modèle comme une fonction mathématique \(f\) : elle reçoit en entrée un vecteur \(x\), qui correspond aux caractéristiques de la personne (âge, sexe, statut marital, etc) et retourne une probabilité \(y=f(x)\).

En Machine Learning, c'est qui particulier en comparaison avec les algorithmes plus classiques, c'est que la fonction \(f\) est construire automatiquement à partir des données. En effet, le Data Scientist ne va plus construire des algorithmes avec des si ... alors ... sinon, mais va utiliser une métrique pour vérifier à quel point l'algorithme est conforme par rapport aux données et à quel point il réussit à donner les bonnes réponses (dans cet exemple, les bonnes probabilités).

Pour répondre à toutes ces interrogations, nous devons donc décortiquer cette fameuse fonction \(f\). Or, c'est justement ce travail qui est difficile, car très souvent, ces fonctions \(f\) sont le résultat d'opérations mathématiques complexes qui peuvent rendre leur interprétation difficile.

Naissance de l'interprétabilité

Au cours des dernières années, les modèles de Machine Learning atteignaient des performances de plus en plus élevées, dépassant parfois les performances réalisées par des humains sur certaines tâches précises. La compétition annuelle ILSVRC, où des équipes de recherche évaluent des algorithmes de traitement d'image sur le jeu de données ImageNet, voyait les meilleurs taux d'erreurs graviter autour de 26%.

En 2012, l'avènement des réseaux de neurones et de l'apprentissage profond, et plus particulièrement les réseaux de neurones convolutifs ont permis d'abaisser le taux d'erreur à 16%. Depuis, les réseaux de neurones sont majoritairement utilisés dans cette compétition et d'autres semblables.

❓ Pourquoi alors c'est si difficile d'interpréter un modèle ?

Les réseaux de neurones sont souvent considérés comme des « boîtes noires », c'est-à-dire des algorithmes dont le fonctionnement est opaque et difficile à interpréter. En effet, du fait du très grand nombre de paramètres (plusieurs dizaines voire centaines de millions), l'interprétation de ces modèles n'est pas faisable. Or, une machine n'a pas la capacité d'interpréter un résultat, car c'est justement toute la difficulté que l'on rencontre au quotidien quand il s'agit de mettre en exergue des réponses ou des décisions à partir de résultats quantitatifs.

Le terme transparence des algorithmes est propre au contexte étudié, et il n'existe pas une définition unique. La transparence peut faire référence à la connaissance de la décision prise par l'algorithme, au degré d'exactitude de la prédiction ou à l'importance des variables sur la prédiction. Christoph Molnar reprend la définition de l'interprétabilité de Tim Miller :

« L'interprétabilité est le degré à quel point un humain peut expliquer de manière cohérente les prédictions du modèle »

Sous cette définition, l'interprétabilité est une partie intégrante de la transparence, qui vise à être capable d'expliquer de manière précise et consistante la prédiction, que ce soit pour une observation ou dans le comportement global de l'algorithme.

Méthodes d'interprétabilité

La grande question, c'est de savoir comment est-ce que l'on va être capable d'interpréter un modèle de Machine Learning. En réalité, il faut plutôt se poser comme question avec quoi et pourquoi interpréter, car en réalité, tous les modèles n'ont pas besoin de méthodes particulières pour être interprétés.

Modèles naturellement interprétables

Que signifie un modèle naturellement interprétable ? Prenons le cas d'une régression linéaire, modèle simple où nous pouvons directement exprimer une quantité comme combinaison linéaire de chaque variables explicative avec des poids \(\beta_j\).

$$y_i= \beta_0 + \sum_{j=1}^p \beta_j x_{ij} + \varepsilon_i$$

Intuitivement, plus \(\beta_j\) est élevé, plus la contribution de la variable \(x_{\bullet j}\) est importante car une variation \(h\) de \(x_{\bullet j}\) augmente la quantité \(y_i\) de \(\beta_j h\). Par cette relation linéaire, nous sommes donc capable de calculer directement l'impact de chaque variable sur la prédiction. De plus, du fait de l'hypothèse de linéarité entre les variables, il est facile d'expliquer comment, pour un individu donné, le résultat a été obtenu (i.e. \(y_i\) a augmenté ou diminué). Enfin, le modèle suppose initialement l'indépendance entre les variables, ce qui permet de considérer les effets croisés entre les variables inexistants.

Chaque variable étant associée à un poids \(\beta_j\), si toutes les variables sont dans la même unité de mesure, cela permet donc de mesure l'importance de chaque variable. Néanmoins, chaque individu possède des caractéristiques différentes : et c'est notamment en multipliant la valeur \(x_{ij}\) d'une variable d'un individu \(x_i\) par le poids \(\beta_j\) que l'on peut caractériser, pour cet individu, l'importance et le rôle de la variable sur la prédiction.

À lire aussi : découvrez notre formation MLOps

Pour ce modèle, pas besoin d'y apporter une méthode d'interprétabilité : sa définition permet directement d'interpréter les résultats.

Modèles moins interprétables

En pratique, la régression linéaire n'est pas toujours adaptée, notamment parce que la relation de linéarité entre la variable réponse et les variables explicatives implique l'indépendances entre les variables explicatives. Or, dans beaucoup de situations, il existe des interactions entre ces mêmes variables explicatives.

Le Data Scientist doit donc se tourner vers un modèle qui permettra d'obtenir de meilleures performances. Dans sa boîte à outils, il dispose de nombreuses possibilités : les méthodes à base d'arbres avec les Random Forest ou les méthodes de boosting (XGBoost, LightGBM), les réseaux de neurones (MLP, Transformers) ou encore les SVM.

Malheureusement, ces modèles qui permettent d'atteindre des performances plus élevées, sont également plus difficilement interprétables. Le modèle XGBoost, par exemple, est construit de manière récursive, et va générer des centaines voire des milliers d'arbres de décision.

Un arbre de décision, cela demande plusieurs minutes pour pouvoir être interprété efficacement. Alors dans le cas où l'on en dispose de plusieurs centaines, la tâche devient impossible (en plus du fait que chaque arbre dépend du précédent à cause de la construction récursive de ces derniers). Pour expliquer la prédiction d'une observation \(x\), il est nécessaire de calculer la sortie de chaque arbre, en sachant que les prédicteurs faibles (les arbres de décision) ne cherchent plus à modéliser la variable réponse, mais les pseudo-résidus dans le contexte de XGBoost. C'est la multiplicité des arbres (associée à d'éventuels arbres profonds) qui rend la compréhension du comportement du modèle quasi-impossible.

Ainsi, au cours des dernières années, la recherche académique s'est donc penchée sur des méthodes d'interprétabilité afin de pouvoir expliquer le comportement et les prédictions des algorithmes. Ces méthodes viennent se greffer autour d'un modèle déjà construit. Deux types de méthodes ont été développées.

Méthode agnostiques

Les méthodes dites agnostiques sont indépendantes du modèle prédictif utilisé. Le principal avantage est leur flexibilité, puisque ces méthodes peuvent être appliquées sans connaissance particulière du modèle prédictif, si ce n'est qu'obtenir la prédiction \(\hat{f}(x)\) pour toute observation \(x\). Ces méthodes agnostiques s'intercalent sur des modèles boîtes noires. Les PDP (Partial Dependency Plot) furent une des premières méthodes d'interprétabilité, en estimant les lois marginales des variables sous des hypothèses d'indépendance entre les variables. Plus récemment, d'autres méthodes telles que LIME ou Kernel SHAP ont été introduites afin de pallier certaines faiblesses des précédentes méthodes et de les adapter pour des modèles plus complexes et plus coûteux en terme de calcul.

Méthode spécifiques

Les méthodes dites spécifiques dépendent du modèle prédictif utilisé. Bien que ces méthodes soient moins flexibles, elles permettent d'obtenir de meilleurs interprétabilité puisqu'elles sont spécifiquement développées pour un modèle prédictif particulier. Ces méthodes ne se reposent pas uniquement sur la prédiction \(\hat{f}(x)\) des observations \(x\), mais utilisent également les propriétés et méthodes de construction d'un modèle pour en extraire le plus d'information quant au comportement que celui-ci adopte. Les réseaux de neurones sont principalement visés par ces méthodes avec DeepLIFT, ou les modèles à base d'arbres avec Tree SHAP.

Niveaux de granularité

Lorsque le terme d'interprétabilité est employé, deux niveaux de granularité peuvent être distingués en classes de méthodes.

• Les méthodes dites locales, où la méthode consiste à expliquer la prédiction d'une observation particulière. Christoph Molnar différencie l'interprétabilité (générale) du modèle et appelle l'explication le fait de pouvoir pleinement expliquer la prédiction pour une observation particulière. DeepLIFT ou Tree SHAP sont des exemples de méthodes locales.
• Les méthodes dites globales, qui cherchent plutôt à expliquer les tendances du modèle sur l'ensemble des prédictions, comme par exemple les lois marginales. PDP ou Tree Interpreter sont des exemples de méthodes globales.

Conclusion

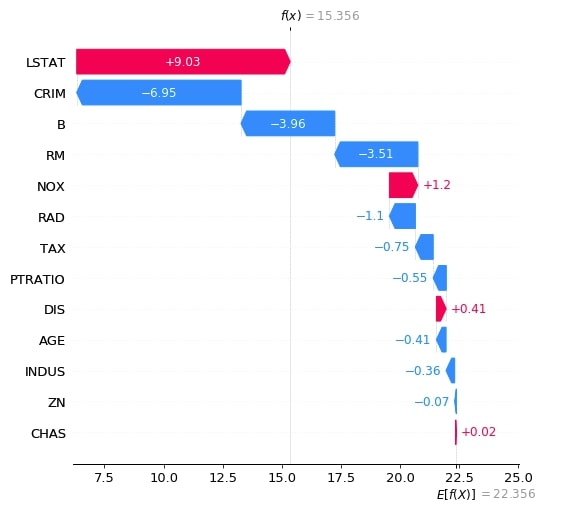
L'interprétabilité est un vaste sujet il y aurait beaucoup de choses à dire qu'il serait impossible de tout résumer en un seul article. Récemment, ce sont les valeurs de Shapley avec la librairie R et Python nommée SHAP qui ont relancé une certaine partie de l'interprétabilité locale, avec cette capacité à attribuer des contributions positives et négatives à chaque variables d'une observation, traduisant de son impact sur la réponse du modèle en prenant en compte les interactions avec les autres variables.

À lire aussi : découvrez notre formation MLOps

Par ailleurs, l'interprétabilité permet aussi de mettre en évidences les problèmes de biais qui interviennent régulièrement dans les modèles de Machine Learning, notamment lorsqu'ils sont calibrés sur des cohortes pas toujours représentative de l'ensemble de la population d'étude. Gardons à l'esprit que comme toujours, en statistiques, il y aura toujours un biais subjectif qu'il est nécessaire de minimiser au maximum.