
Par Équipe Blent
Data Scientist
Publié le 25 janv. 2022
Catégorie Machine Learning
Algorithme k-means : comment ça marche ?
L'algorithme des k-means (ou bien k-moyennes) est l’un des algorithmes d’apprentissage non supervisé les plus simples et les plus populaires. Il permet d’analyser un jeu de données afin de regrouper les données « similaires » en groupes (ou clusters). Ce principe est applicable dans divers domaines de l'industrie comme le domaine du marketing pour la segmentation des clients, analyse des réseaux sociaux, etc. Cela introduit des notions qui se cachent derrière l'algorithme importantes à découvrir et à comprendre.
Dans cet article, nous examinerons la notion du regroupement (clustering) et nous allons détailler le fonctionnement de l'algorithme k-means, en quoi son utilisation et ses applications sont variées ainsi que les moyens utiles pour l’optimiser.
Notion du regroupement (clustering)
Lorsque l'on cherche à s'informer à propos de quelque chose, comme des livres, une approche possible pourrait être de chercher des groupes ou des collections significatives plus ou moins semblables. Par exemple, on pourra organiser ces derniers par auteurs, ou bien par genre. Une autre personne pourra choisir de les organiser par date de publication.
La façon dont on choisit de regrouper ses éléments permettra de s'informer d'avantages à propos de chacune des observations individuellement. On pourra même créer des groupes qui n'existaient pas tout en combinant des critères bien choisis.
À lire aussi : découvrez notre formation MLOps
De même en Machine Learning, nous devons séparer nos données en groupes pour les comprendre. Il existe deux types de méthodes d’apprentissage :
- Si les données sont étiquetées, il s'agit d'une classification, et les données sont regroupées selon leurs étiquettes (ou labels). On appelle cela l'apprentissage supervisé.
- Si les données ne sont pas étiquetées, il s'agit d'un regroupement (clustering). Le principe c'est de séparer les données en groupes homogènes ayant des caractéristiques communes. On appelle cela l'apprentissage non supervisé.
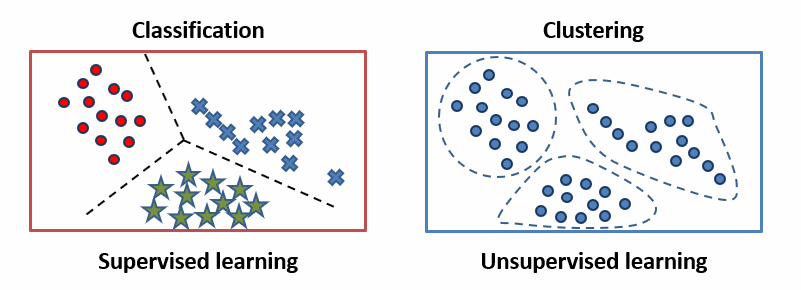
Dans le deuxième cas, on cherche à tirer des références à partir des données en utilisant des méthodes et des métriques de son choix. L'algorithme des k-means est donc un exemple d'apprentissage non supervisé.
Le nombre de groupes (clusters) représenté par la variable \(k\) n'est pas connu : c'est le Data Scientist qui est censé le préciser en fonction de son jeu de données, en estimant par lui-même le nombre de groupe qui existerait dans le jeu de données.
Principe de fonctionnement de l'algorithme k-means
Le cas d’usage le plus classique pour les méthodes de clustering est la segmentation de bases de clients. Nous allons considérer l'exemple d'une clientèle d'une banque.
Cette banque veut fournir des offres de carte de crédit à ses clients. Actuellement, les équipes marketing de la banque examinent les détails de chaque client, et à partir de ces renseignements, décident quelle offre devrait être faite à quel client.
À lire aussi : découvrez notre formation MLOps
Cette méthode prendra énormément de temps et de main-d'œuvre. Ce qui sera plus logique est efficace, ce serait d'utiliser l'algorithme k-means pour regrouper les clients. On prendra deux caractéristiques en premier pour simplifier l'exemple : l'âge et le revenu annuel.
Visuellement, les clients peuvent se séparer en 4 groupes distincts :
- Un premier groupe (en violet) : c'est le groupe des clients qui sont dans leurs vingtaines ayant un revenu annuel élevé (entre 120k et 140k).
- Un deuxième groupe (en orange) : c'est le groupe des clients qui sont dans leurs trentaines/quarantaines ayant un revenu annuel moyen (entre 120k et 80k).
- Un troisième groupe (en bleu foncé) : c'est le groupe des clients dont l'âge varie entre 40 et 60 ayant un revenu annuel moyen (entre 120k et 80K).
- Un dernier groupe (en bleu clair) : c'est le groupe des clients dont l'âge varie entre 80 et 100 ayant un revenu annuel bas (entre 0k et 40K).

La banque peut maintenant préparer quatre stratégies ou offres différentes, une pour chaque groupe au lieu de créer des stratégies différentes pour chaque client. Cela réduira l’effort ainsi que le temps.
Mais comment les groupes sont-ils choisis réellement ? Comment savoir quel élément à mettre dans tel et tel groupe et comment choisir le nombre de groupes optimale pour son jeu de données ?
Détails de l'algorithme k-means
Prenons un exemple simple avec les données réparties sous cette configuration.

Visuellement, un humain peut distinguer trois groupes, mais la machine ne peut pas les voir, car les données dessus sont simplement des points, et les nombres affectés n'ont aucune signification réelle.
On cherche alors à construire des groupes homogènes à partir de ces points.
On commencera par spécifier manuellement la valeur de \(k\), le nombre de groupes qui seront générés par l'algorithme. \(k\) est généralement choisi aléatoirement au début (sauf en cas de connaissance approfondie sur le contexte), et on essayera ensuite de trouver la valeur de \(k\) optimale selon les premiers résultats que l'on obtiendrait, ou alors en utilisant des méthodes d'optimisation.
Dans notre cas, nous choisissons \(k=3\). Ces 3 points de données « prototypes » s'appellent des centroïdes et représentent les centres des groupes. Au début, ils seront choisis et placés aléatoirement comme suit.
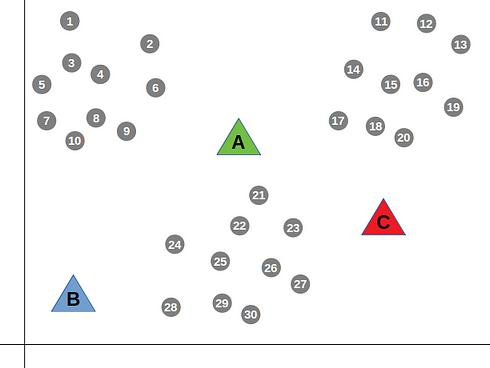
L’algorithme passe par les points de données un par un, en mesurant la distance entre chaque point par rapport aux trois centroïdes (A, B et C). L’algorithme regroupe ensuite le point de données avec le centroïde le plus proche (c'est-à-dire celui le plus proche en terme de distance la distance).
Par exemple, le point n°21 appartiendra au groupe de A car il est plus proche au centroïde A que C.
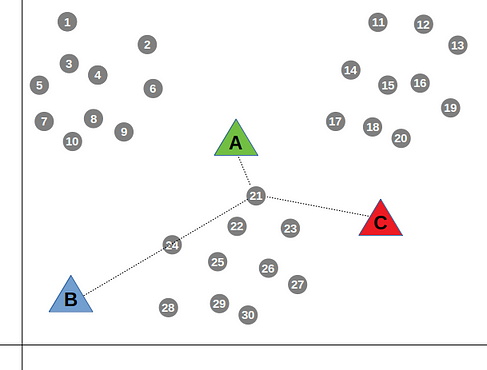
Puisque l'on vient d'affecter chaque point à un des 3 groupes, les centres ne sont plus les mêmes ! Il faut donc recalculer les 3 nouveaux centroïdes qui seront les centres de gravité de chaque groupe calculé dans l'étape précédente.
On répète ces étapes jusqu’à ce que les nouveaux centroïdes soient stabilités, et ne changent plus de groupe.
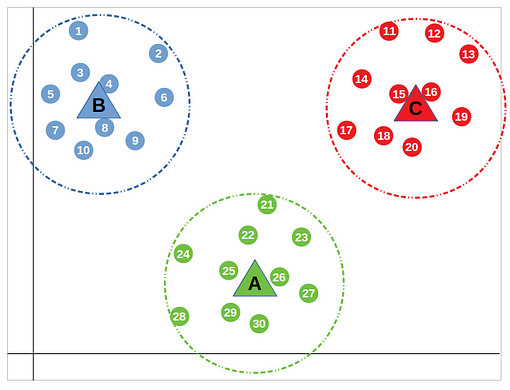
Quelle métrique utiliser pour évaluer la distance entre les points et les centroïdes ?
Pour pouvoir regrouper un jeu de données en \(k\) groupes distincts, l’algorithme k-means a besoin d’un moyen pour comparer le degré de similarité entre les différentes observations.
L'algorithme des k-means fait généralement intervenir la distance euclidienne. Soient deux groupes d'éléments \(p=(p_1, \dots, p_n)\) et \(q=(q_1, \dots, q_n)\), alors la distance \(d\) entre les points \(p\) et \(q\) se calcule avec cette formule.
$$d\left( p,q\right) = \sqrt {\sum _{i=1}^{n} \left( q_i-p_i\right)^2 }$$Dans l'exemple précédent, nous avons calculé la distance euclidienne entre un point et chacun des centroïdes, puis nous l'avons associé au centroïde le plus proche, c’est-à-dire celui avec la plus petite distance. Ce calcul est effectué pour chacun des points du jeu de données.
Quel est le nombre de clusters à choisir ?
Lorsque la taille du jeu de données est importante, nous n'avons pas forcément d'hypothèses sur les données, et par la suite suite, nous ne pouvons pas choisir la valeur de \(k\) intuitivement. Comment faire dans ce cas ?
Il existe deux méthodes empiriques qui nous permettent de déterminer une valeur de \(k\) optimale lorsque l'on ne sait pas exactement combien de clusters il existerait dans le jeu de données.
Méthode de coude
Il existe une méthode populaire connue sous le nom de « The Elbow method » ou la méthode du coude qui est utilisée pour déterminer la valeur optimale de \(k\). L’idée de base derrière cette méthode se décompose en plusieurs étapes.
- On lance l'algorithme k-means avec différentes valeurs de \(k\).
- On calcule la distance moyenne entre les points et leurs centroïdes respectives au carré. On appellera cette valeur WSS (Within Sum of Squares)
- On place les différents nombres de clusters \(k\) en fonction de la valeur WSS sur un graphique.
Nous obtenons alors une visualisation en forme de coude.
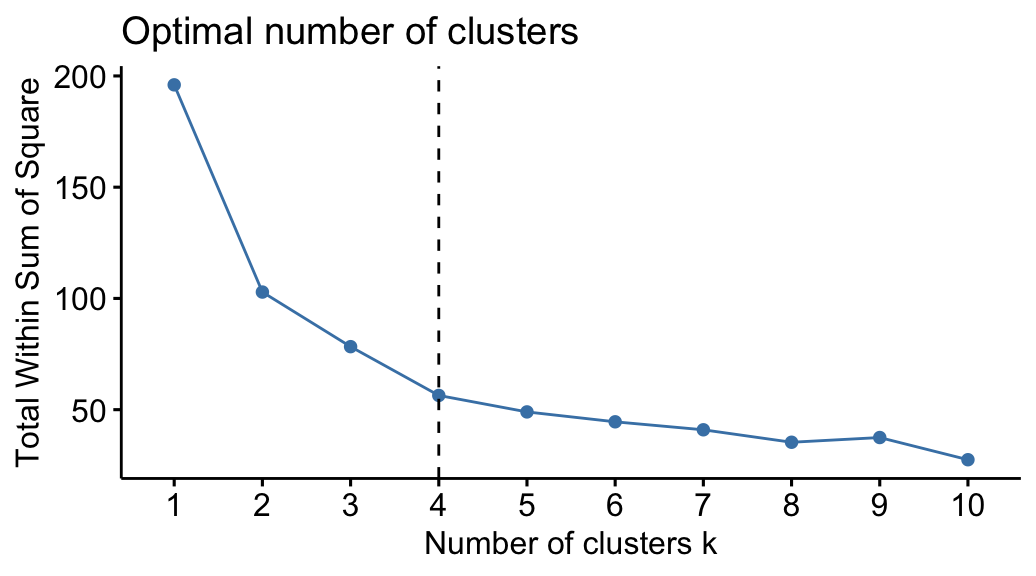
L’emplacement d’une courbe (coude) dans le graphique est généralement considéré comme un indicateur du nombre approprié de groupes. Les distances ne varient plus rapidement après cette inflexion, c'est-à-dire qu'une augmentation de \(k\) n'aura pas un grand effet sur les distances entre les points de données et leurs centroïdes respectives.
Par conséquent, nous pouvons estimer à cet endroit, que l'on arrive à la valeur optimale de \(k\).
Méthode de silhouette
La méthode de silhouette est également une méthode pour trouver le nombre optimal de clusters. Le coefficient de silhouette est une mesure de la similitude d’un point de données à l’intérieur d’un groupe par rapport à d’autres groupes.
Ce coefficient doit être calculer pour chaque point du jeu de données. Pour trouver ce coefficient du i-ème point :
- On commence par calculer \(a_i\) : la distance moyenne de ce point avec tous les autres points dans les mêmes clusters.
- Ensuite, on calcule \(b_i\) : la distance moyenne de ce point avec tous les points du cluster le plus proche de son cluster.
- Finalement, on calcule \(s_i\) (coefficient de silhouette) pour ce i-ème point en utilisant la formule ci-dessous.
On choisira une plage de valeurs \(k\) candidates, puis on lancera l'algorithme k-means pour ces valeurs de \(k\) en calculant à chaque fois le coefficient de silhouette moyen.
À lire aussi : découvrez notre formation MLOps
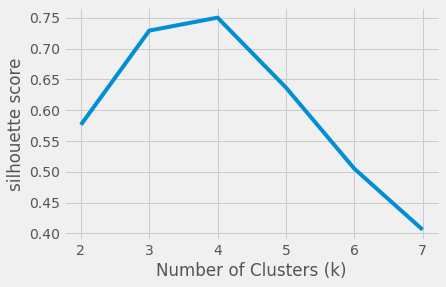
Dans l'exemple qui suit, on remarque que le coefficient de silhouette est maximal pour \(k=4\), le nombre de clusters adéquats dans ce cas alors est 4.
Quand utiliser l'algorithme k-means ?
Avec ce que nous venons de voir, l'algorithme k-means s'adapte à de nombreuses situations de clustering.
- L'algorithme k-means est un modèle prédictif très simple et non hiérarchique : il ne nécessite donc pas beaucoup de temps d’exécution. Il est aussi rapide et efficace en termes de coûts de calcul. Cela en fait la solution meilleure dans le cas de données volumineuses.
- Il ne peut être exécuté qu'avec des données numériques. Il est donc déconseillé de l'utiliser avec des données d'autres types.
- Dans la situation où le jeu de données est de grande dimension, c'est-à-dire lorsque le nombre de variables ou d’attributs est beaucoup plus élevé que le nombre d’observations, un modèle de Machine Learning aura besoin d'un énorme ensemble d'entrainement (train set) pour apprendre. Cet algorithme est le meilleur choix dans ce cas.
- Enfin, les k-means sont fréquemment utilisés dans le domaine de l'imagerie médicale, la segmentation des couleurs et parfois pour la détection des anomalies.
Néanmoins, il y a aucune garantie de convergence avec l'algorithme des k-means. En effet, puisque l'étape d'initialisation calcule des centroïdes de manière aléatoire, il se peut qu'aucun groupe ne se stabilise à long terme, et donc qu'aucune convergence ne se produire.
L'algorithme des k-means est l’un des algorithmes de clustering les plus populaires et généralement la première chose que les Data Scientists appliquent pour résoudre des tâches de regroupement. Il est non seulement simple et facile à comprendre mais aussi rapide et économique en matière de coût de calcul.
Vous souhaitez vous former au MLOps ?
Articles similaires

20 sept. 2022
Hugging Face est une startup française qui s'est fait connaître grâce à l'infrastructure NLP qu'ils ont développée. Aujourd'hui, elle est sur le point de révolutionner le domaine du Machine Learning et traitement automatique du langage naturel. Dans cet article, nous allons présenter Hugging Face et détailler les taches de base que cette librairie permet de réaliser. Nous allons également énumérer ses avantages et ses alternatifs.
Équipe Blent
Data Scientist
Lire l'article

12 juil. 2022
spaCy est une bibliothèque open-source pour le traitement avancé du langage naturel. Elle est conçue spécifiquement pour une utilisation en production et permet de construire des applications qui traitent et comprennent de grands volumes de texte.
Équipe Blent
Data Scientist
Lire l'article

4 juil. 2022
Un auto-encodeur est une structure de réseaux neuronaux profonds qui s'entraîne pour réduire la quantité de données nécessaires pour représenter une donnée d'entrée. Ils sont couramment utilisés en apprentissage automatique pour effectuer des tâches de compression de données, d'apprentissage de représentations et de détection de motifs.
Équipe Blent
Data Scientist
Lire l'article

60 rue François 1er
75008 Paris
Blent est une plateforme 100% en ligne pour se former aux métiers Tech & Data.
Organisme de formation n°11755985075.

Data Engineering
IA Générative
MLOps
Cloud & DevOps
À propos
Gestion des cookies
© 2025 Blent.ai | Tous droits réservés
