Réseaux récurrents (RNN) : on vous explique tout

Les réseaux neuronaux alimentent un large éventail d’applications d’apprentissage profond dans différentes industries avec différents cas d'utilisation, du traitement du langage naturel (NLP) à la vision par ordinateur.

Mais lorsqu’il s’agit de données séquentielles ou chronologiques, les réseaux de neurones traditionnels ne peuvent pas être utilisés pour l’apprentissage et la prédiction. Il faut un mécanisme qui permet de conserver les données antérieures ou historiques pour prévoir les valeurs futures. Les réseaux neuronaux récurrents ou les RNNs en abrégé sont une variante des réseaux neuronaux artificiels qui peuvent traiter des données séquentielles et peuvent être entrainés pour détenir les connaissances sur le passé. Les RNNs sont couramment utilisés dans les domaines de l'apprentissage automatique, de traitement de langage naturel et de reconnaissance de formes.

Dans cet article, nous allons introduire les réseaux de neurones récurrents et leur architecture, les types de modèles Deep Learning se basant sur des RNNs et des exemples de modèles se basant sur ce type de réseaux.

Qu'est-ce qu'un réseau de neurone récurrent ?

Les RNNs sont idéales pour résoudre des problèmes où la séquence est plus importante que les éléments individuels eux-mêmes. On les utilise généralement pour traiter des données séquentielles, qui peuvent être des données chronologiques ou des données textuelles de n’importe quel format.

À lire aussi : découvrez notre formation MLOps

Les séquences sont des objets dont chaque élément possède un ordre, une position, une inscription dans le temps. Par exemple, dans une phrase, chaque mot vient dans un certain ordre et il est prononcé sur un intervalle de temps distinct de celui des autres.

En raison de leur mémoire interne, les RNNs peuvent se souvenir de choses importantes au sujet de l’entrée qu’ils ont reçue, ce qui leur permet d’être très précis dans la prédiction de ce qui vient après. Dans un réseau de neurones standard, l’information ne se déplace que dans une direction, de la couche d’entrée, en passant par les couches cachées, à la couche de sortie. L’information circule directement dans le réseau et ne touche jamais un nœud deux fois.

Dans un RNN, l’information passe par une boucle. Lorsqu’il prend une décision, il tient compte des données actuelles et de ce qu’il a appris des données reçues précédemment.

Imaginons que nous avons un réseau de neurones classique et donnons-lui le mot Bonjour comme entrée et il traite le mot caractère par caractère. Au moment où il atteint le caractère j, il a déjà oublié b, o et n, ce qui rend presque impossible pour ce type de réseau neuronal de prédire quelle lettre viendrait ensuite.

Un RNN, cependant, est capable de se souvenir de ces caractères en raison de sa mémoire interne. Il produit la sortie, la copie et la boucle dans le réseau.

Pour obtenir plus de couches de calcul pour être en mesure de résoudre ou d’estimer des tâches plus complexes, la sortie du RNN pourrait être alimentée dans un autre RNN, ou n’importe quel nombre de couches de RNNs.

Architecture d'un RNN

Considérez l'unité neuronal simple à propagation avant ou feedforward ce dessous à droite. Cette unité a une seule couche cachée. \({X}_{t}\) est son entrée et \({Y}_{t}\) est sa sortie à un instant précis t. Si nous voulons créer une unité récurrente simple à partir de cette dernière, alors tout ce que nous devons faire est de créer une connexion de retour de la couche cachée à elle-même pour accéder à l’information de l'instant t-1. Cette boucle de rétroaction implique un retard d’une unité de temps. Donc, l’une des entrées de \({H}_{t}\) est \({H}_{t-1}\), tour à tour la couche cachée a à chaque fois deux entrées, sa valeur actuelle et sa propre dernière valeur. En résumé, cette boucle de rétroaction permet à l’information de se transmettre d’une étape du réseau à l’autre et agit ainsi comme mémoire dans le réseau.

Le diagramme ci-dessous illustre l’architecture avec les poids :

À partir de la figure ci-dessus, nous pouvons écrire les équations ci-dessous :

\left{\begin{matrix} \mathbf{H}t = \phi(\mathbf{X}_t \mathbf{W}{x} + \mathbf{H}{t-1} \mathbf{W}{h} + \mathbf{b}_h) \ \mathbf{O}t= \mathbf{H}{t} \mathbf{W}_{o} + \mathbf{b}_t \end{matrix}\right. \(\)

• La quantité \({Y}_{t}\) est la sortie de la couche de récurrence en t. Cela est donc un vecteur de taille h.
• L'état \({H}_{t}\) qui n'est pas utilisé par en sortie, mais qui interviendra dans le calcul pour la date suivante. C'est d'ailleurs la raison pour laquelle on attribue le nom d'état caché, car \({H}_{t}\) n'est utilisée que pour le calcul et ne sort pas des neurones de la couche.
• \({W}_{x}\) les poids en entrée de la couche récurrente.
• \({W}_{h}\) les poids à l'intérieur des neurones pour l'état caché.
• \({W}_{0}\) les poids en sortie de la couche récurrente.

À l'itération t, on calcule \({H}_{t}\) en faisant intervenir l'état caché de la précédente itération \({H}_{t-1}\) et l'entrée actuelle \({X}_{t}\) à partir des poids, pour ensuite calculer la sortie \({Y}_{t}\). L'état caché actuel \({H}_{t}\) sera ensuite utilisée pour la prochaine séquence.

Avec cette relation de récurrence des \({H}_{t}\), les RNNs prennent tout leur sens pour modéliser des séquences avec une relation de dépendance selon t : \({H}_{t}\) va préserver l'information de l'élément précédent de la même séquence. La sortie \({Y}_{t}\) va dépendre de la variable latente \({H}_{t}\), qui elle-même dépens de \({X}_{t}\) et de son état précédent \({H}_{t-1}\). Ce sont les poids qui, en fonction de leurs valeurs, vont permettre de créer et quantifier un lien entre deux (voir plus) éléments successifs de la séquence.

Un réseau neuronal récurrent peut être considéré comme plusieurs copies d’un réseau feedforward, chacun transmettant un message à un successeur.

Maintenant, qu'est-ce qui se passe si nous déroulons la boucle ? Imaginons que nous avons une séquence de longueur 5, si nous devions déplier le RNN dans le temps comme il n’a pas de connexions récurrentes du tout, alors nous obtenons ce réseau neuronal feedforward avec 5 couches cachées comme indiqué dans la figure ci-dessous.

Un réseau récurrent est donc équivalent an un réseau feedforward de taille égale à la longueur de séquence traitée et aux poids égaux.

Les types de réseaux récurrents

L’architecture RNN peut varier selon le problème que nous essayons de résoudre. De ceux avec une seule entrée et sortie à ceux avec beaucoup. Voici quelques exemples d’architectures RNN qui peuvent nous aider à mieux comprendre cela.

One To One

Le type le plus simple de RNN est One-to-One, il a une seule entrée et une seule sortie. Ses tailles d'entrée et de sortie sont fixes et agit comme un réseau neuronal traditionnel. L’application de One-to-One peut être utilisée dans la classification d’image.

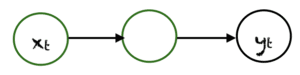
One To Many

One-to-Many est un type de RNN qui donne plusieurs sorties lorsqu’il est donné une seule entrée. Il prend une taille d’entrée fixe et donne une séquence de sorties de données. Ses modèles peuvent d'appliquer à la génération de musique et sous-titrage d’image.

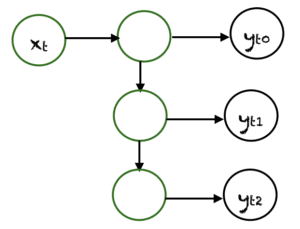
Many To One

Many-to-One est utilisé lorsqu’une seule sortie est requise à partir de plusieurs unités d’entrée ou d’une séquence d’entre elles. Il faut une séquence d’entrées pour afficher une sortie fixe. L’analyse des sentiments est un exemple courant de ce type de réseau neuronal récurrent.

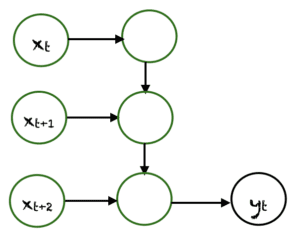
Many To Many

Many-to-Many est utilisé pour générer une séquence de données de sortie à partir d’une séquence d’unités d’entrée. Ce type de RNN est divisé en deux sous-catégories :

À lire aussi : découvrez notre formation MLOps

1. Taille égale des unités : Dans ce cas, le nombre d’unités d’entrée et de sortie est le même. Une application commune peut être trouvée dans Name-Entity Recognition.

2. Taille inégale des unités : Dans ce cas, les entrées et les sorties ont un nombre d’unités différent. Son application peut être trouvée dans la traduction automatique.

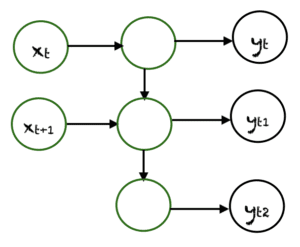
Limitations et variantes des RNNs

Les réseaux neuronaux récurrents souffrent d’un problème appelé disparition de gradient, qui est également un problème commun pour d’autres algorithmes de réseaux neuronaux. Le problème de la disparition du gradient est le résultat d’un algorithme appelé rétroropagation qui permet aux réseaux neuronaux d’optimiser le processus d’apprentissage.

En bref, le modèle de réseau neuronal compare la différence entre sa sortie et la sortie désirée et renvoie ces informations au réseau pour ajuster des paramètres tels que les poids à l’aide d’une valeur appelée gradient. Une plus grande valeur de gradient implique de plus grands ajustements aux paramètres, et vice versa. Ce processus se poursuit jusqu’à ce qu’un niveau satisfaisant de précision soit atteint.

Les RNNs exploitent l’algorithme de rétroropagation dans le temps (BPTT) où les calculs dépendent des étapes précédentes. Cependant, si la valeur du gradient est trop petite dans une étape pendant la rétroconversion, la valeur sera encore plus petite dans l’étape suivante. Cela entraîne une diminution exponentielle des gradients à un point où le modèle cesse d’apprendre.

Ceci est appelé le problème de disparition de gradient et provoque les RNNs à avoir une mémoire à court terme : les sorties antérieures ont de plus en plus peu ou pas d’effet sur la sortie actuelle.

Le problème du gradient de fuite peut être résolu par différentes variantes des RNNs. Deux d’entre eux sont :

• LSTM (appelés Long Short-Term Memory) : Ils sont capables de se souvenir des entrées sur une longue période de temps. C’est parce qu'ils contiennent des informations dans une mémoire, un peu comme la mémoire d’un ordinateur. Le LSTM peut lire, écrire et supprimer des informations de sa mémoire. Dans cette mémoire, on décide à chaque fois de stocker ou de supprimer des informations en fonction de l’importance qu’elle accorde à l’information. L’attribution de l’importance se fait par des poids, qui sont également appris par l’algorithme.
• GRU (Gated Recurrent Units) : Ce modèle est similaire aux LSTM car il permet aussi de résoudre le problème de mémoire à court terme des modèles RNN. Pour résoudre ce problème, GRU intègre les deux mécanismes de fonctionnement de porte appelés Update gate et Reset gate: les portails de réinitialisation et de mise à jour sont concrètement des vecteurs qui contrôlent les informations à conserver et à négliger.

Les réseaux neuronaux récurrents sont un outil polyvalent qui peut être utilisé dans une variété de situations. Ils sont employés dans diverses méthodes de modélisation linguistique et de génération de texte. Ils sont aussi employés dans la reconnaissance vocale. Cependant, ils ont un défaut. Ils sont lents à entrainer et ont de la difficulté à apprendre les dépendances à long terme.