
Par Équipe Blent
Data Scientist
Publié le 11 févr. 2022
Catégorie Machine Learning
SVM : Support Vector Machine
SVM (Support Vector Machine ou Machine à vecteurs de support) est un algorithme d’apprentissage automatique supervisé qui peut être utilisé pour les problèmes de classification ou de régression. Toutefois, il est surtout utilisé dans les problèmes de classification.
Il était extrêmement populaire à l’époque où il a été développé, dans les années 1990, et continue de l'être car il produit une précision significative avec un minimum de puissance de calcul.
Le SVM joue aussi un rôle important dans la reconnaissance des modèles qui est l'un des domaines de recherche les plus populaires et actif de nos jours. Dans cet article, nous allons détailler les différents concepts du SVM ainsi que préciser la manière optimale pour l'utiliser.
Fonctionnement de l'algorithme SVM
Le principe des SVM consiste à ramener un problème de classification ou de discrimination à un hyperplan (feature space) dans lequel les données sont séparées en plusieurs classes dont la frontière est la plus éloignée possible des points de données (ou marge maximale).
On prendra un exemple simple de classification pour mieux comprendre de quoi il s'agit. On dispose d'une population composée de 50% de femme et 50% d’hommes. En utilisant un échantillon de cette population, on veut créer un ensemble de règles qui nous guideront dans la classification de sexe pour le reste de la population.
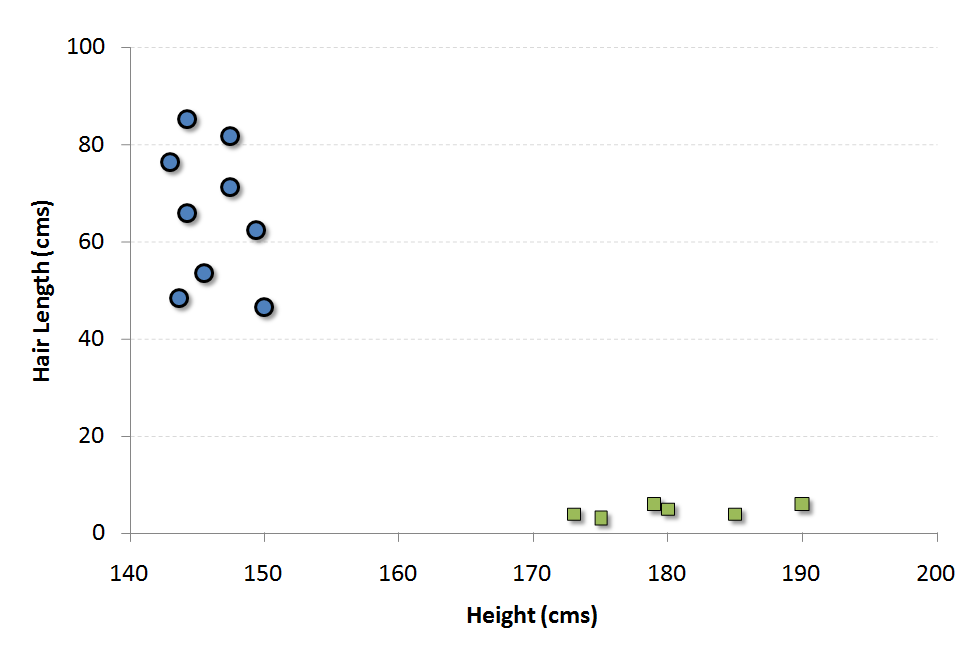
On suppose que les deux facteurs de différenciation identifiés sont : la taille de l’individu et la longueur des cheveux. Voici un diagramme de dispersion de l’échantillon:
À lire aussi : découvrez notre formation MLOps
Les cercles bleus dans le graphique représentent les femmes et les carrés verts représentent les hommes. Visuellement, on peut distinguer ces deux classes comme suit :
- Les hommes de cette population ont une taille moyenne plus élevée.
- Les femmes de cette population ont des cheveux plus longs.
Supposons qu'on a un individu avec la hauteur 180 cm et la longueur des cheveux 4 cm qu'on devra classer. Intuitivement, on va le placer avec les hommes.
Comment peut-on amener la machine à comprendre ce type de principes et l'appliquer sur de nouveaux éléments n'appartenant pas à la population de base?
À l'aide d'un classificateur de la famille SVM cela est possible à travers un hyperplan séparateur bien choisi.
On commence tout d'abord par projeter chaque élément de données dans l’espace \(n\)-dimensionnel (où \(n\) représente le nombre de caractéristiques présents dans le jeu de données) avec la valeur de chaque caractéristique étant la valeur d’une coordonnée particulière.
Ensuite, on effectue la classification en trouvant l’hyperplan qui différencie très bien les deux classes. Dans le cas de la population ci-dessus, plusieurs choix se présentent.
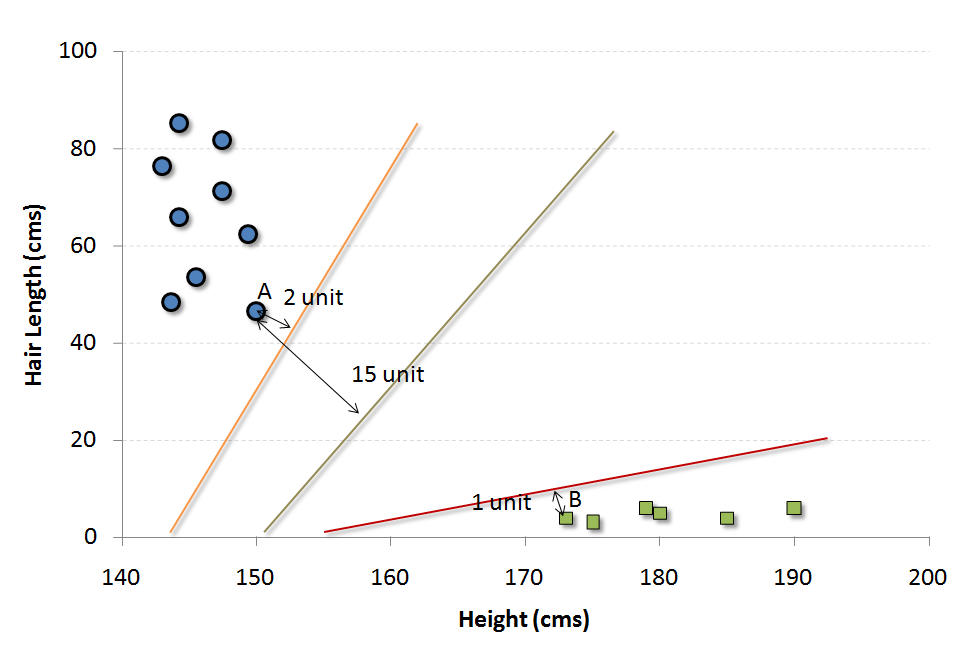
Comment décider quel est le meilleur hyperplan à choisir pour ce jeu de données ?
L'approche la plus adéquate dans ce cas est de trouver la distance minimale de la frontière par rapport a l'élément de la population le plus proche (cet élément peut appartenir à n’importe quelle classe).
Par exemple, la frontière orange est la plus proche des cercles bleus. Et le cercle bleu le plus proche est à 2 unités de la frontière. Une fois que nous avons ces distances pour toutes les frontières, nous choisissons simplement la frontière avec la distance maximale (à partir du vecteur de support le plus proche).
Sur les trois frontières indiquées, nous voyons que la frontière noire est la plus éloignée de l'élément le plus proche (c.-à-d. 15 unités).
Cas particuliers
Cet exemple présentait des données faciles à séparer à l’aide d’un hyperplan linéaire. Parfois les données sont dispersées dans l'espace d'une manière qui rend la séparation difficile visuellement et linéairement. Que faire donc si on ne trouve pas une frontière propre qui sépare les classes?
Plusieurs cas peuvent se présenter.
Première situation
Commençons par cette situation.
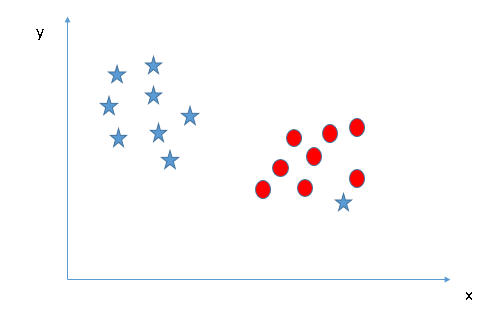
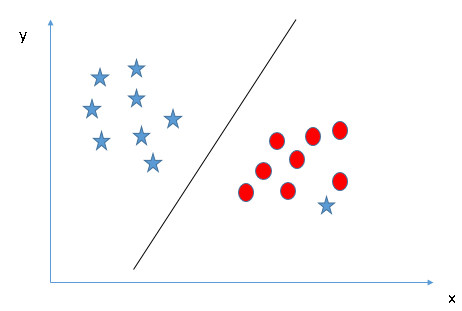
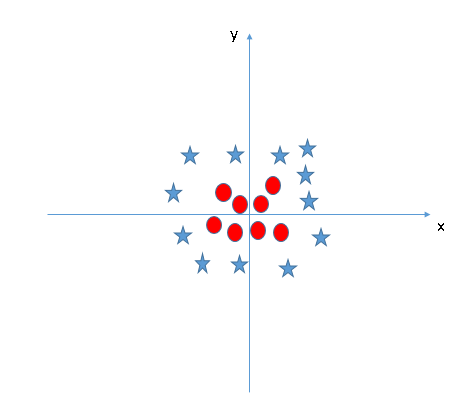
Ici, on remarque que nous sommes incapable de séparer les deux classes en utilisant une ligne droite, car l’une des étoiles se trouve dans le territoire d’une autre classe (cercle) comme une valeur aberrante.
L’algorithme SVM a une fonctionnalité pour ignorer ce genre de valeurs et trouver l’hyperplan qui a la marge maximale. La classification SVM est donc robuste aux valeurs aberrantes.
Deuxième situation
Dans le scénario ci-dessous, nous ne pouvons pas avoir d’hyperplan linéaire entre les deux classes.
SVM peut résoudre ce problème en introduisant une troisième dimension.
Ici, on va ajouter une nouvelle dimension à partir des deux précédentes : \(z=x^2 + y^2\). Ainsi, on a pris en entrée un espace de faible dimension et l'a transformé en un espace de dimension supérieure. Maintenant, projetons les points de données sur les axes \(x\) et \(z\).
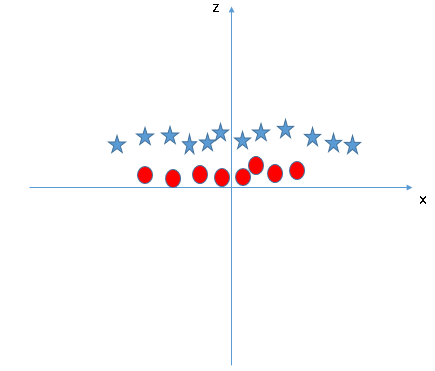
Dans le graphique que l'on a obtenu, toutes les valeurs de \(z\) sont toujours positives parce que \(z\) est la somme carrée de \(x\) et \(y\).
Dans le tracé original, les cercles rouges apparaissent proches de l’origine des axes \(x\) et \(y\), ce qui conduit à une valeur inférieure de \(z\) et à une étoile relativement éloignée de l’origine.
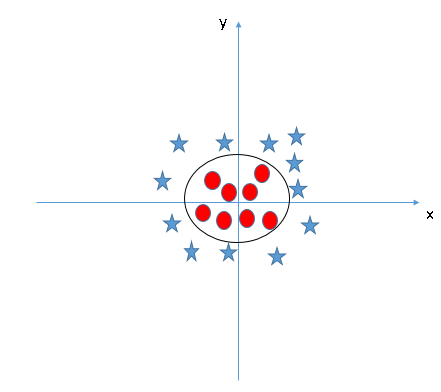
Quand on regarde l’hyperplan dans l’espace d’entrée d’origine, il ressemble à un cercle.
SVM multi-classe
Comme nous l'avons déjà mentionné, le nombre de dimensions de l'espace dépend du nombre de classes, dans le cas oµ le jeu de données en question présente plusieurs classes, l'application du SVM devient compliquée. tout d'abord c'est parce que cet algorithme ne supporte pas la classification multi-classe, mais plutôt la classification binaire.
Pour résoudre ce problème, il existe deux approches possibles.
- La première méthode consiste à projeter les éléments du jeu de données dans l’espace pour obtenir une séparation linéaire mutuelle entre chaque deux classes. C’est ce qu’on appelle une approche One-to-One, qui décompose le problème multiclasse en plusieurs problèmes de classification binaire. Un classificateur binaire pour chaque paire de classes.
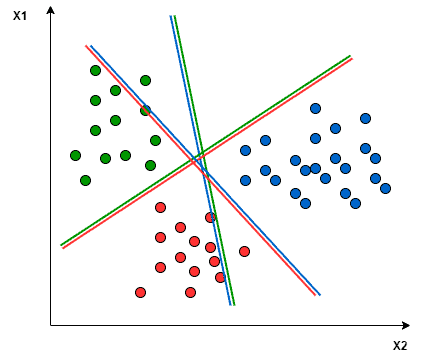
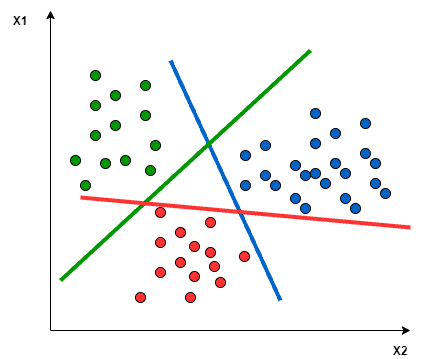
- Une autre approche que l’on peut utiliser est One-to-Rest. La répartition dans ce cas est définie par un classificateur binaire : pour chaque classe, nous avons besoin d’un hyperplan pour séparer une classe et toutes les autres à la fois. Cela signifie que la séparation tient compte de tous les points, les divisant en deux groupes : un groupe pour les points de classe et un groupe pour tous les autres points. Par exemple, la ligne verte tente de maximiser la séparation entre les points verts et tous les autres points à la fois.
Hyperparamètres du SVM:
L'implémentation algorithmique du SVM sous Scikit-Learn requiert un certain nombre d'hyperparamètres.
- kernel : Il représente le type de noyau à utiliser (
rbfest la valeur par défaut). Choisir le bon noyau est crucial, et chaque noyau à ses propres avantages. Par exemple, dans le cas ou le jeu de données est séparable linéairement, il est préférable d'utiliser le noyaulinear. dans le cas ou le jeu de données présente plusieurs classes, le meilleur choix c'est lerbf(Radial Basis Function) car il supporte la projection dans des espaces à grande dimension. Notons bien que ce choix est plus douteux en puissance de calcul. On utilise fréquemment le noyaupolylorsqu'on travaille avec des images. - C : C'est le paramètre de régularisation de précision. Si le C est élevé, on choisira un hyperplan à plus petite marge, de sorte que le taux de fautes de classification sera plus faible. L'utilisation de cet hyperparamètre contribue énormément à éviter le sur-apprentissage.
- degree : il n’est utilisé que si le noyau choisi est
polyet définit le degré du polynôme. - probability : c’est un paramètre booléen et s'il est vrai, alors le modèle renverra pour chaque prédiction, le vecteur de probabilités d’appartenir à chaque classe de la variable réponse. Donc, essentiellement, il donnera une évaluation pour chaque prédiction.
- gamma: il n’est utilisé que si le noyau choisi est
rbf. Le paramètregammadéfinit jusqu’à quel point l’influence d’un seul exemple d’entraînement est importante. Cela signifie que sigammaest élevé, on considérera seulement les points proches de l’hyperplan sinon on considérera les points à plus grande distance.
À lire aussi : découvrez notre formation MLOps
Quand doit-on utiliser le SVM ?
- SVM est le choix optimal lorsqu'on travaille avec un jeu de données présentant un grand nombre de classes. Il est fréquemment utilisé pour la reconnaissance faciale, la classification de texte (NLP) et la classification d'image.
- Il faut faire très attention au sur-apprentissage avec cet algorithme, surtout dans le cas ou le nombre de classes est supérieur au nombre d'observations ( cela peut être évité avec la régularisation des hyperparamètres
Cetgamma) - Le SVM utilise un sous-ensemble de points de formation dans la fonction de décision (appelés vecteurs de soutien ou support vectors), de sorte qu’il est également efficace en mémoire et efficace pour les données volumineuses.
- Les transformations de données complexes ( passage de 2D à 3D par exemple) et le plan limite (frontière) qui en résulte sont très difficiles à interpréter. C’est pourquoi on l’appelle souvent une boîte noire. Ce modèle n'est pas vraiment interprétable.
Le SVM est l'un des modèles Machine Learning non seulement les plus simples, mais aussi l'un des plus performants. C'est pourquoi les Data Scientists le favorisent et l'utilisent toujours surtout pour des problèmes de classification.
Vous souhaitez vous former au MLOps ?
Articles similaires

20 sept. 2022
Hugging Face est une startup française qui s'est fait connaître grâce à l'infrastructure NLP qu'ils ont développée. Aujourd'hui, elle est sur le point de révolutionner le domaine du Machine Learning et traitement automatique du langage naturel. Dans cet article, nous allons présenter Hugging Face et détailler les taches de base que cette librairie permet de réaliser. Nous allons également énumérer ses avantages et ses alternatifs.
Équipe Blent
Data Scientist
Lire l'article

12 juil. 2022
spaCy est une bibliothèque open-source pour le traitement avancé du langage naturel. Elle est conçue spécifiquement pour une utilisation en production et permet de construire des applications qui traitent et comprennent de grands volumes de texte.
Équipe Blent
Data Scientist
Lire l'article

4 juil. 2022
Un auto-encodeur est une structure de réseaux neuronaux profonds qui s'entraîne pour réduire la quantité de données nécessaires pour représenter une donnée d'entrée. Ils sont couramment utilisés en apprentissage automatique pour effectuer des tâches de compression de données, d'apprentissage de représentations et de détection de motifs.
Équipe Blent
Data Scientist
Lire l'article

60 rue François 1er
75008 Paris
Blent est une plateforme 100% en ligne pour se former aux métiers Tech & Data.
Organisme de formation n°11755985075.

Data Engineering
IA Générative
MLOps
Cloud & DevOps
À propos
Gestion des cookies
© 2025 Blent.ai | Tous droits réservés
