
Par Équipe Blent
Data Scientist
Publié le 15 mars 2022
Catégorie Machine Learning
Algorithme t-SNE : comment ça fonctionne ?
La réduction de dimension est une technique très populaire, généralement utilisée par les Data Scientists pour améliorer la performance des algorithmes de Machine Learning, surtout lorsqu'on travaille avec des jeux de données à plusieurs variables. Elle permet d'éliminer les variables corrélées qui ne contribuent à aucune prise de décision. Il existe plusieurs approches pour ce faire, dont t-SNE (t-distributed Stochastic Neighbor Embedding), un algorithme d’apprentissage non supervisé connu notamment pour sa capacité à faciliter la visualisation des données non linéaires ayant beaucoup de descripteurs.
Dans cet article, nous allons détailler la notion de réduction des dimensions, le fonctionnement de l'algorithme t-SNE, comment et quand faut-il l’utiliser.
Notion de réduction de dimension en Machine Learning
La réduction de dimension est un processus étudié en mathématiques et en informatique. Il consiste à prendre des données dans un espace de grande dimension, et à les remplacer par d'autres dans un espace de dimension inférieure, mais qui contiennent encore la plupart des informations contenues dans le grand ensemble.
Autrement dit, on cherche à construire moins de variables tout en conservant le maximum d'informations possible.
En Machine Learning, ce processus de traitement de données est crucial dans certains cas, parce que les jeux de données plus petits sont plus faciles à explorer, exploiter et à visualiser, et rendent l’analyse des données beaucoup plus facile et plus rapide.
Cette étape est importante aussi dans les cas du sur-apprentissage et des données très éparses (fléau de la dimensionnalité), qui nécessitent beaucoup de temps et de puissance de calcul pour les étudier.
En utilisant un espace de plus petite dimension, on obtient des algorithmes plus efficaces, ainsi qu'un panel de solutions plus réduit.
À lire aussi : découvrez notre formation MLOps
Pour ce faire, on peut agir de deux manières différentes.
Supprimer des variables
Cette technique consiste à éliminer tout simplement des variables estimées d'être redondantes ou peu importantes pour la prise de décision. Parmi les méthodes se basant sur cette technique, on peut citer :
Les régularisations de certains modèles
La régression pénalisée (par exemple la régularisation de type L1/Lasso et L2/Ridge) est un type de régularisation qui force le modèle à atteindre un équilibre entre performance et nombre de dimensions retenues. Ils permettent d’effectuer la sélection de variable selon les résultats d'une fonction de pénalité qui attribue un poids à chaque variable. Les modèles à vecteurs de support (SVM) sont régularisé de cette manière.
La régularisation des modèles basées sur des arbres de décision, y compris les forêts aléatoires ou le Gradient Boosting, est aussi une méthode se basant sur le même principe. On réduit la profondeur des arbres et des branches en évitant, lors de la sélection de la variable optimale pour la scission d’un nœud, de choisir une variable qui soit trop corrélée à celle sélectionnée dans la scission précédente.
La sélection des variables selon leur relation avec la variable de sortie
Il s'agit de sélectionner des variables les plus importantes à utiliser dans les algorithmes Machine Learning avant que le modèle soit entraîné avec. Concrètement, plusieurs tests statistiques peuvent être effectués pour sélectionner les caractéristiques qui ont la relation la plus forte avec la variable de sortie comme le coefficient de corrélation, la MAD (moyenne absolue des différences), ou le ratio de dispersion.
Combiner des variables
Cette approche consiste à combiner deux ou plusieurs variables afin d’obtenir un plus petit nombre de nouvelles variables plus expressives et moins redondantes sans supprimer des parties du jeu de données. Pour mieux comprendre on prendra les deux exemples suivants :
L'ACP (Analyse des composantes principales)
C'est une technique qui vise à transformer des variables corrélées en nouvelles variables décorrélées en projetant les données dans le sens de la variance croissante. Les variables avec la variance maximale seront choisies comme les composants principaux. Regardant le repère ci-dessous :

Dans le premier repère, que la variance des données selon l'axe rouge est grande. Si on projette les points sur cet axe, ils auront tous des coordonnées différentes, mais on continue à pouvoir distinguer les points les uns des autres, en utilisant cet axe comme unique dimension, on réduit la dimension de nos données (de 2 à 1).
LDA (Analyse discriminante linéaire)
Cette méthode est similaire à l'ACP, sauf que les points de données sont projetées cette fois sur de nouveaux axes de sorte que ces nouvelles composantes maximisent la séparabilité entre les catégories tout en maintenant la variation au sein de chacune des catégories à une valeur minimale.
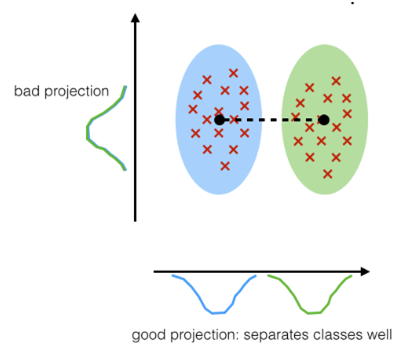
Il existe d'autres techniques de réductions de dimensions qui peuvent être citées en guise d'exemple comme la réduction avec la cartographie isométrique, les auto-encodeurs, la réduction par décomposition de matrices ou bien t-SNE.
À lire aussi : découvrez notre formation MLOps
Fonctionnement de t-SNE
\(t\)-Distributed Stochastic Neighbor Embedding (t-SNE) est une technique **non supervisée et non linéaire** principalement utilisée pour l’exploration, la visualisation et la réduction des dimensions de données de haute dimension. En d'autres mots, le rôle de cet algorithme est la **réduction de la dimensionnalité non linéaire**. Cela signifie qu'il permet de séparer les données qui ne peuvent pas être séparées par une ligne droite. Il donne une idée ou une intuition de la façon dont les données sont organisées dans un espace de grande dimension et par conséquent, il produit des groupes séparés et bien définis. Une fois, on a compris ses données, t-SNE se charge de les compresser en les projetant dans un espace de faible dimension (2D ou 3D).Prenons comme exemple les données bien simples suivants afin d'expliquer étape par étape le fonctionnement de l'algorithme du t-SNE.

Visuellement, le jeu de données se compose de quatre groupes distincts. Tous les éléments sont projetés dans un repère orthonormé de dimension 2.
En ce qui suit, on va essayer de réduire la dimension de nos données (de 2 à 1) en utilisant le t-SNE.
- La première étape consiste à créer la distribution de probabilité qui représente les similitudes entre voisins en choisissant un point de données aléatoire (dans notre cas le point x1) et en calculant la distance euclidienne entre ce point et d’autres points de données. Cette distance représente le degré de similarité entre les points. C'est-à-dire que les points de données proches du point de données sélectionné obtiendront plus de valeur de similarité et les points de données qui sont loin du point de données sélectionné obtiendront moins de valeur de similarité.
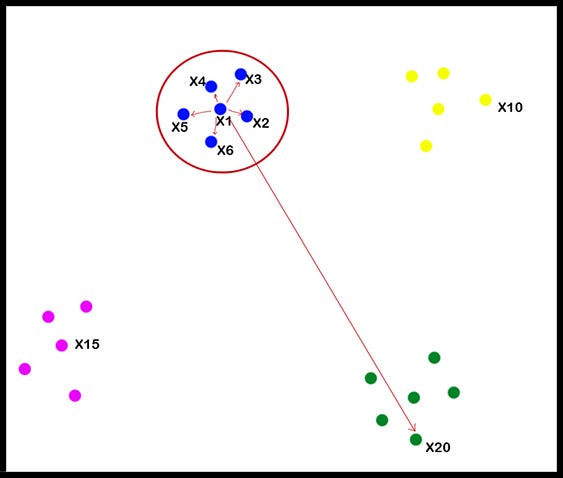
Avec les valeurs de similarité, on va créer une matrice de similarité (\(S1\)) pour chaque point de données. En regardant l'image ci-dessus, on peut dire que les éléments \(X2, X3, X4, X5\), et \(X6\) sont les voisins de \(X1\), ils obtiendront une valeur plus élevée dans la matrice de similarité \(S1\) de \(X1\). D’autre part, \(X20\) est situé loin de \(X1\). Donc, il obtiendra une valeur inférieure dans \(S1\).
L'étape suivante consiste à convertir la distance de similarité calculée en probabilité conjointe selon la distribution normale. Et puis créer un espace de faible dimension (dans notre cas 1D) avec le même nombre de points que dans l'espace d'origine. Les points doivent être répartis au hasard sur cet espace parce qu'au début on ne connait pas leur coordonnées idéales.

Ensuite, on refait tous les mêmes calculs qu’on a faits pour les points de données de dimensions supérieures aux points de données de dimensions inférieures disposés de façon aléatoire à nouveau. Mais dans cette étape, on va calculer la probabilité selon la distribution de Student et on créera une matrice de similarité (\(S2\)).
Maintenant, l’algorithme compare \(S1\) avec \(S2\) et fait la différence entre \(S1\) et \(S2\) en utilisant un algorithme de descente de gradient exécuté avec Kullback Leibler Divergence (KL Divergence) entre les probabilités conditionnelles. Pour faire simple, on peut traiter ce gradient comme une répulsion et une attraction entre les points. Un gradient est calculé pour chaque point et décrit à quel point il doit être « fort » et la direction qu'il doit choisir. Cette divergence KL aide t-SNE à préserver la structure locale des données en minimisant la différence entre les deux distributions par rapport aux emplacements des points de données. Cela revient à minimiser l’écart entre les distributions de probabilités entre l’espace d’origine et l’espace de plus petite dimension.
Quand et comment utiliser le t-SNE ?
Le t-SNE est un algorithme très intelligent qui permet d'éviter le sur-apprentissage et de simplifier les données. Il s'adapte à des situations de réductions de dimensions précises.
- Cet algorithme gère efficacement et intelligemment les données non linéaires et les données qui présentent des valeurs aberrantes ou extrêmes contrairement à L'ACP qui est un algorithme linéaire.
- Il faut faire attention à ne pas utiliser le t-SNE avec des jeux de données volumineux, parce qu'il implique beaucoup de calculs. Il est particulièrement lent et gourmand en matière de puissance de calcul.
- Le t-SNE est non déterministe, parfois, on n’obtiendra pas exactement la même sortie chaque fois qu'on l’exécute, bien que les résultats sont susceptibles d’être similaires. Il est donc efficace pour comprendre et décortiquer des données complexes, mais pas vraiment pour l'entrainement des modèles Machine Learning puisqu'il peut changer de résultats d'une exécution à une autre.
- Il peut être utilisé pour comprendre et interpréter les réseaux de neurones convolutifs (CNN) qui sont généralement des boites noires. Comment faire cela ? Il suffit de visualiser les sorties de certaines couches et les visualiser, cela aide beaucoup à comprendre ce qui se passe à l’intérieur du réseau.
À lire aussi : découvrez notre formation MLOps
Bien qu'il fonctionne très bien, certaines améliorations permettent à cet algorithme de faire encore mieux. Par exemple, la perplexité qui est le paramètre principal contrôlant l’ajustement des points de données dans l’algorithme. Il est conseillé d'ajuster ce paramètre lors de l'exécution du t-SNE. Il doit toujours être inférieur au nombre de points de données.
- Peu de perplexité signifie qu'on se soucie de la structure locale et se concentre sur les points de données les plus proches.
- Grande perplexité signifie qu'on se soucie de la structure globale du jeu de données.
En bref, t-SNE est une technique de réduction de la dimensionnalité qui peut être appliqué sur des ensembles de données linéaires et non linéaires. Bien qu'il soit relativement nouveau, plusieurs Data Scientists l'utilisent pour comprendre et visualiser des données complexes et de haute dimension.
Vous souhaitez vous former au MLOps ?
Articles similaires

20 sept. 2022
Hugging Face est une startup française qui s'est fait connaître grâce à l'infrastructure NLP qu'ils ont développée. Aujourd'hui, elle est sur le point de révolutionner le domaine du Machine Learning et traitement automatique du langage naturel. Dans cet article, nous allons présenter Hugging Face et détailler les taches de base que cette librairie permet de réaliser. Nous allons également énumérer ses avantages et ses alternatifs.
Équipe Blent
Data Scientist
Lire l'article

12 juil. 2022
spaCy est une bibliothèque open-source pour le traitement avancé du langage naturel. Elle est conçue spécifiquement pour une utilisation en production et permet de construire des applications qui traitent et comprennent de grands volumes de texte.
Équipe Blent
Data Scientist
Lire l'article

4 juil. 2022
Un auto-encodeur est une structure de réseaux neuronaux profonds qui s'entraîne pour réduire la quantité de données nécessaires pour représenter une donnée d'entrée. Ils sont couramment utilisés en apprentissage automatique pour effectuer des tâches de compression de données, d'apprentissage de représentations et de détection de motifs.
Équipe Blent
Data Scientist
Lire l'article

60 rue François 1er
75008 Paris
Blent est une plateforme 100% en ligne pour se former aux métiers Tech & Data.
Organisme de formation n°11755985075.

Data Engineering
IA Générative
MLOps
Cloud & DevOps
À propos
Gestion des cookies
© 2025 Blent.ai | Tous droits réservés
